3D rendering is a fundamental aspect of computer graphics, involving the transformation of three-dimensional points into two-dimensional coordinates. I provide visualizations of this process by applying projection and rotation matrices to four platonic solids: cube, octahedron, icosahedron, and dodecahedron.
The Concept Behind Platonic Rotation
3D rendering is a classic example of applied linear algebra where three-dimensional coordinates (x, y, z) are mapped to two-dimensional coordinates (x, y) via transformation matrices. Using OpenCV, I simulated the application of projection and rotation matrices to four platonic solids, showcasing their rotations in real-time.
What Platonic Rotation Does
I used OpenCV's built-in functions line(...) and circle(...) along with the Mat array class. The following animation provides an example of the rotations:
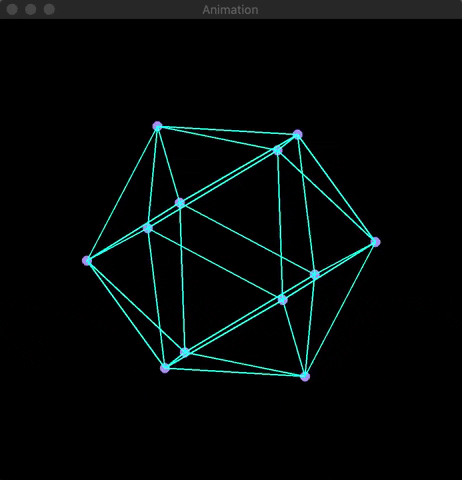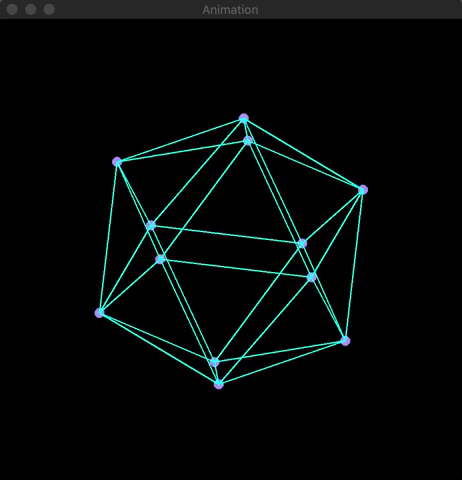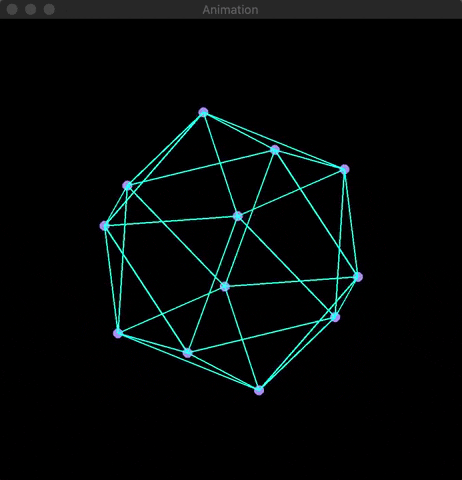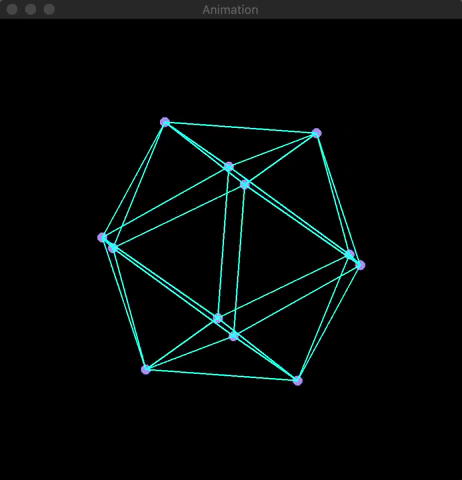
The Math
Step One: Rotation
To rotate the 3D coordinates, each x-y-z coordinate is converted into a 1x3 matrix and then multiplied by the rotation matrices. Here are the rotation matrices used:
These matrices, along with the three-dimensional coordinate matrix, are represented in my code as two-dimensional vectors:
vector<vector<float>> rotationX{{1,0,0},{0,cos(angle),-sin(angle)},{0,sin(angle),cos(angle)}};
vector<vector<float>> rotationY{{cos(angle),0,-sin(angle)},{0,1,0},{sin(angle),0,cos(angle)}};
vector<vector<float>> rotationZ{{cos(angle),-sin(angle),0},{sin(angle),cos(angle),0},{0,0,1}};
The order of multiplication affects the rotation animation. In my code, the rotation sequence is first along the Y axis, then the X axis, and finally the Z axis:
vector<vector<float>> rotated = matmul(rotationY, points[i]); // rotates along Y axis
rotated = matmul(rotationX, rotated); // then rotates along X axis
rotated = matmul(rotationZ, rotated); // finally rotates along Z axis
Step Two: Orthographic Projection
Finally, the 1x3 x-y-z coordinate matrix is converted into two-dimensional coordinates using the orthographic projection matrix:
The orthogonal projection matrix is represented in my code as follows:
vector<vector<float>> projection{{1,0,0},{0,1,0}};
Running the Code (for Mac/Linux)
To run the code, you need to have OpenCV set up on your personal computer. Refer to this guide for OpenCV installation instructions. Ensure that your opencv.pc file is located in your pkgconfig folder.
Compile the code by navigating to the cloned repository in the terminal and running:
g++ $(pkg-config --cflags --libs opencv) -std=c++11 [name of file].cpp -o runThen, run the program with:
./runConclusion
Platonic Rotation offers a fascinating look into the application of matrix multiplication in 3D rendering, demonstrating the rotations of various platonic solids. This project highlights the importance of understanding matrix operations in computer graphics and provides a visual representation of these mathematical concepts.
Explore the source code and contribute to the project on GitHub.